As a preamble to this section, we mention Archimedes’ principle that tells us that “the lifting force exerted on a body immersed in a liquid is equal to the weight of the liquid that the body has been squeezed out.” And it is precisely this lifting force that carries the ship and its cargo.

The displacement of a ship means the weight of the water mass as the ship’s underwater body displaces. Archimedes’ principle also tells us that the weight of the displaced water mass is equal to the ship’s total weight.
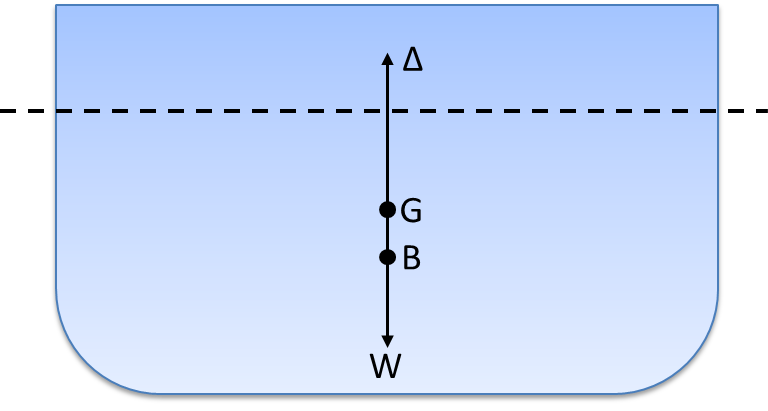
When properly loaded the ship sails on a steady course and on a quiet and calm day with neither wind nor waves the vessel is in equilibrium. Two equal and along the same manufacturing line directed against each other forces affecting the vessel. One force, lift force Δ, attacks in the depth of focus B and is directed upwards. The second downward force which attacks the ship’s center of gravity G is denoted by W.

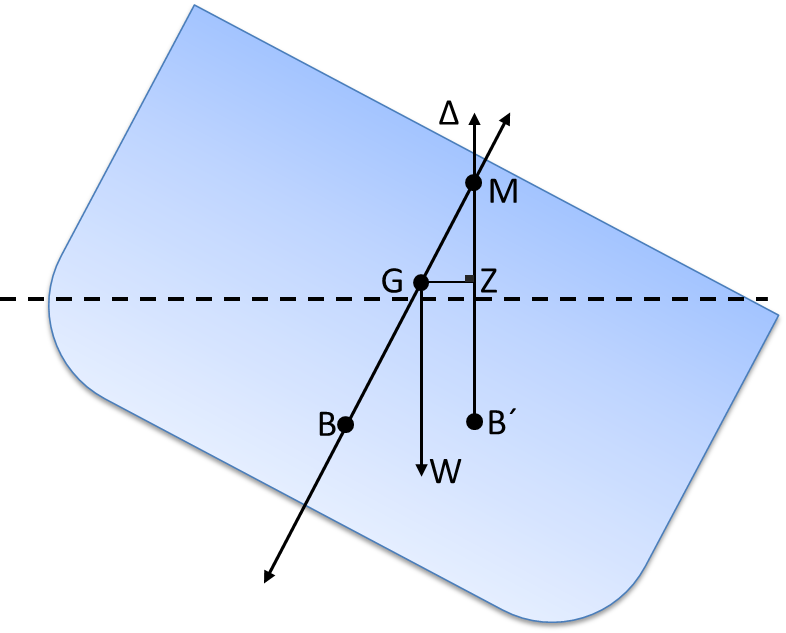
If the ships pitch is changed (assuming rough sea and wind coming in at the ship side) the equilibrium will be affected while a righting moment that want to straighten the vessel will occur. This part consists of W and the distance Δ GZ from each other. The point M where the lift force cutting the vessel center line, we find meta-center. The distance between point G and point M is called the metacentric height and gives a good picture of the ship’s stability. See figure below.

Where M is located depends on what ship’s underwater body is shaped at a certain depth. Where G is located depends on how the ship is designed to some extent, but more on how the ship is loaded with cargo. If heavy cargo is loaded on deck the ship’s center of gravity G will be displaced upwards. This means that GM reduces in length. If GM is reduced so will the GZ with the effect that the righting moment becomes smaller which leads to the fact that the ship’s stability is impaired.

Here is another article about stability!